Introduction

"The underlying physical laws necessary for the mathematical theory of a large part of physics and the whole of chemistry are thus completely known, and the difficulty is only that the exact application of these laws leads to equations much too complicated to be soluble." -- P.A.M. Dirac, 1929

Virtually every paper on computational chemistry begins with this famous quote by the British theoretical physicist and one of the pioneers of quantum mechanics, Paul Adrien Maurice Dirac (1902-1984). His 1929 quote that we now “know” chemistry but that the mathematics are not “soluble” (able to be solved) serves as the foundation for this and every other paper in computational chemistry. In this case, to know chemistry means that we can describe it using detailed mathematics

Computational chemistry, sometimes referred to as molecular modeling or computational quantum chemistry, represents the newest method of conducting chemical research, joining its well-established colleagues of observational, experimental, and theoretical chemistry. Given the increasing prominence of computation in the chemical profession, this paper looks to provide support for this simple premise:

An understanding of and ability to use the technologies, techniques, and tools of computational chemistry are as important for chemistry students as those technologies, techniques and tools found in the traditional “wet” laboratory.

A casual scanning of the scientific literature supports this premise. Computational articles are easy to find in journals such as the Journal of Computational Chemistry (Wiley Publishers) and the Journal of Computer Aided Chemistry (Japan), but also appear regularly in Science, Nature, and the Journal of Chemical Education. Given that reality, it is critically important that chemical educators at all levels, beginning with pre-college students, include computation as an essential skill. We as chemical educators would never ignore the teaching of basic concepts in acid-base chemistry or fail to provide opportunities for students to learn how to perform a titration or other basic laboratory skill. Likewise, we can no longer ignore the prominence of computation as one of the essential tools in the arsenal of the research chemist. Computational chemistry must be included in our list of what it means to know chemistry. Our students must be as familiar with the Schrödinger equation as they are with the ideal gas law, and must be able to perform a vibrational analysis of a compound as readily as they are able to find its experimental melting point. Likewise, especially in this day of high-stakes testing at the pre-college level, we must expect the student to demonstrate his or her proficiency in computational chemistry on end-of-course exams, AP exams, and other evaluation tools. Without that expectation, students will not be exposed to these tools and methods, and, as a result, will not be adequately prepared for careers as scientists.

One might ask: why are computational methods not a more integral part of the modern chemical curricula at the undergraduate or pre-college levels? A simple (and perhaps simplistic) reason is offered: teachers teach the way they were taught. Those of us in our 40s and 50s are of that generation where computers were not as powerful, nor as ubiquitous, as they are today. In my own experience as a computational chemist, the calculations that I can now perform on a handheld PDA or a low-end laptop were only possible on big mainframes or supercomputers when I began my career as a computational chemist in the late 1980s.

Regardless of why computation is not more prominent, the chemical education profession must begin a serious effort to increase the importance of computing in chemistry. Organizations such as the National Science Foundation (NSF) have funded a considerable number of programs at the undergraduate and pre-college levels to increase an understanding of computation in all disciplines of science, including chemistry. Programs such as the SuperQuest Supercomputing Challenge (1987), the National Computational Science Leadership Program (1998), and other NSF-funded programs have looked to explore what students are capable of doing and how teachers might be prepared to increase the role of computing in the science classrooms. NSF’s concern about increasing the number of computationally savvy science students has even reached into non-traditional audiences. My own funding from NSF has included significant funds to determine how to incorporate computational science into classrooms with deaf children by developing the sign language vocabulary needed to communicate the concepts of computation to that audience.

The remainder of this paper will provide a short description of computational chemistry, followed by a description of efforts being made to improve and increase the teaching of computational chemistry at the pre-college level.

Computational Chemistry Simplified

Simply put, computational chemistry is the merging of chemistry, computing, and mathematics. In computational chemistry (again, a term synonymous with molecular modeling), a molecule or reaction mechanism is studied by applying one or more mathematical theories to determine one or more properties or behaviors of a molecule or chemical system.

In teaching my students, I have a number of “sound-bite” phrases and sayings that help them to remember what they are trying to accomplish, and how they might interpret the results. The first, and most important of these, is a daily mantra, and comes from the industrial statistician George Box: “All models are wrong, some are useful”. It is important for students to remember that all descriptions of chemical systems are simply models, and all make assumptions about those systems that are not found in reality. Today’s students have to be warned about accepting answers simply because the computer says it’s right.

In teaching computational chemistry as a formal class and in my integration of computational chemistry into core chemistry classes, I also use the “SPA” framework on an almost daily basis: Structure-Property-Activity. I teach my students that to really know a molecule or molecular system, they must understand the structure of the molecule(s), the property of a molecule (defined as those characteristics of the molecule that the molecule has by itself), and the activity of a molecule (those properties that a molecule exhibits in the presence of other molecules).

I also use a number of analogies to help students understand both the basics of computational chemistry as well as some of the more challenging concepts. I suggest to students that there are five considerations that the computational chemist needs to make in applying computation to the study of a molecule or a molecular system. By way of analogy to cooking chicken, I suggest that the chef needs to know what s/he is trying to prepare, the form of the raw chicken, what ingredients s/he has available, what cooking tools s/he has, and what recipes s/he knows or can find. Analogously, the computational chemist needs to know what s/he is trying to compute, the geometry of the molecule or molecular system, the mathematics available in a given software package, what software is available to that user, and what computational theories the user has and knows. The chart below captures these considerations and their application to both chicken and molecules. Over a span of almost 20 years of teaching computational chemistry to pre-college students, I have found that this analogy provides a great deal of comfort to students when they become overwhelmed with the complexities of a particular computational challenge:

By way of illustration, one of the first computations students perform is a vibrational analysis of water. All molecules vibrate in the infrared, and the number of vibrations can be predicted by various laws such as the “3N-6” rule, where N is the number of atoms (producing, in this case, three vibrations).

In this study, students begin by building the water molecule and performing a basic optimization of the geometry to determine the lowest energy value of the molecule. Based on this optimization, they are able to determine the bond lengths and angles of the molecule. They then perform a vibrational analysis of the molecule using the semi-empirical software package MOPAC¹ (Molecular Orbital PACkage), with a PM3 mathematical parameterization set. 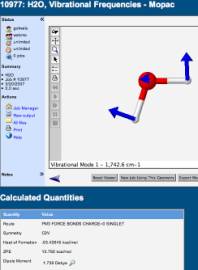Once the calculation (known as a “job” in computational chemistry parlance) is completed, the results are available for analysis. A screen capture of some of the results is shown below. We can see one of the vibrations of water (scissoring), and some of the properties of the molecule: energy in terms of heat of formation (kcal/mol), dipole moment (Debyes), and its molecular symmetry (C₂V). It should be noted that the students can see an animation of the vibrations, not just the static image shown in this screen capture. The students can also rotate the molecule, zoom in or out, and otherwise see the molecule from a variety of perspectives. For this particular calculation (vibrational frequency), students can also view calculated IR spectra of the water molecule. I teach them that, depending on the choice of mathematical theory (known in the community as a model chemistry), the data from the IR spectra is skewed by about 11% from that of experimental vibrational frequencies (“all models are wrong....”). They learn how to compare computed results with that of experimental results by using resources such as the Computational Chemistry Comparison and Benchmark Database from the National Institute of Standards and Technology (NIST, http://srdata.nist.gov/cccbdb/). Lively discussions on who is “right” (experimentalists or “computationalists”) are not uncommon.

Other data generated by this job includes partial charges and bond orders. Also available to the students is the raw output of the job, which provides a significant amount of data, much of it beyond the realm of most pre-college students (and teachers).

On the North Carolina High School Computational Chemistry Server² (described in more detail later in this paper), students build molecules, submit jobs, and analyze results using an inexpensive Web/Java-based interface known as WebMO³. This interface provides an easy-to-use connection between the user and the research-grade quantum chemistry software packages, such as MOPAC, Gaussian 03⁴ and GAMESS⁵ (General Atomic and Molecular Electronic Structure System).

Readers are strongly invited to “take a spin” on the server by going to http://chemistry.ncssm.edu, logging on as guest (password: guest), and, in the vernacular, performing a Hartree-Fock (HF) 3-21G vibrational analysis of water. Detailed instructions are provided on the main page in the lab “Case Study: Vibrational Frequencies of Water”. The guest account allows users to run very small jobs to get a sense of what computational chemistry is like, but not run production (research) level calculations. Resources for that are described later in this paper.

Assuming that the reader has a basic sense of what computational chemistry is, we now turn to pedagogical issues. How does the chemistry educator use computational chemistry in the classroom? Over the past 20 years, I have taken three approaches to academic uses of computational chemistry, all at the pre-college level:

Integration into the “traditional” classroom curricula
Establishment of a stand-alone course in computational chemistry
Establishment of a research program in computational chemistry

Each of these approaches is described in this paper. Prior to that discussion, however, a broad-scope picture of pedagogy is perhaps useful. Computational science educators call this, with some degree of tongue in cheek, the “associative law” of computational chemistry education:

Computational (chemistry education)

(Computational chemistry) education

This “law” suggests the following. There are two ways we can use computation in chemistry. The first is as a tool for teaching the same topics that are taught using more traditional methods: atomic and molecular structures, acid/base chemistry, kinetics, thermochemistry, organic chemistry, and the like. Conversely, we also teach students about the technologies, techniques and tools of computation. What is a semi-empirical method? How do ab initio methods differ, both in their mathematics and in the quality of the computation? I believe that learning about computational chemistry methods is as important as using those methods to learn about chemistry.

Classroom Integration

My introduction to computational chemistry came as a result of teaching chemistry to very advanced students at the Blair Magnet Program at Montgomery Blair High School (Silver Spring, MD) in the late 1980s. It was clear that these students had no conceptual idea of what was happening at the molecular level, especially when addressing topics such as reaction dynamics, activation energies, and chemical kinetics. Through work with the NSF on a number of high school computational science programs, we were able to see the power of computing in providing students with a way to see and study scientific events that happen too fast, too slow, are too large, or are too small. My experiences with those programs were life changing: I became a full-time computational science educator, working at a supercomputing center in North Carolina and with various NSF-supported computational science education organizations.

Now back in the classroom full-time at the North Carolina School of Science and Mathematics (NCSSM, http://www.ncssm.edu, a state-supported residential school for high school juniors and seniors with a strong interest and aptitude for science and math), I integrate computational opportunities on a regular basis in my AP Chemistry course. The approach I take is described as “just in time”. By this I mean that when the students are struggling with some concept, I will bring computation in as a tool for them to better understand that concept. I do not take time to provide them with a lengthy background overview of computational chemistry, its varied methods and mathematics, or even its implementation. I introduce enough information for them to use computational chemistry as a problem-solving tool. For example, this coming week (Sept 10, 2007) in AP Chemistry we are beginning a discussion of aqueous solutions, and I will use a computational analysis of water to introduce the concepts of molecular structure, bonding, and properties such as dipole moment and heats of formation. As this is their first exposure to computational chemistry, I will use the chicken analogy to help them have a sense of what they are doing and why, but the focus is on using computation to learn all we can about water. In other words, computational (chemistry education).

During the course of the year, I routinely have the students perform computational labs, in addition to the standard wet lab activities advocated (mandated?) by the AP Chemistry curriculum. Many of the AP topics are difficult ones for students, especially those related to atomic and molecular structures. For example, Lewis dot structures and their significance are conceptually very difficult. With computation, we can mathematically calculate and visualize lone pair orbitals. A lab (currently in development) looks to help students understand why some molecules violate the octet rule. Without computing, students have to take it on faith that not all molecules follow the rules. In looking at bonding, students can perform molecular and natural bond orbital calculations and visualize sigma (s) and pi (p) bonds. In reaction kinetics and thermochemistry, we can computationally determine the activation energies (E_a) of a reaction, and determine the rate constant for a particular reaction. We use computation with our organic chemistry students to help them develop a more intuitive feel for organic structures and functional groups, and perform computational experiments to determine the pKa values for carboxylic acids. We teach a course at NCSSM in environmental chemistry, and students use computation to look at the degradation rates of atmospheric pollutants. In this activity, students compare their calculations to the experimentally determined kinetics of a variety of environmentally relevant compounds.

In the process of integrating computation into the traditional classroom, we make every effort to use the right tool for the right job, and work hard to help our students understand why and how we make those decisions. Most of my colleagues are traditional experimental chemists, and I am the only computational chemist on staff. As such, we work collaboratively to help students decide if a problem is better solved by running an experiment in the lab, by running a “comp chem job”, or by some combination of the two. The experimental chemists, of course, want to address every problem in the lab, while I tend to run to my computer at the drop of a hat. Because, however, we care about the best interests of our students, my colleagues will sometimes advocate computation while I will sometimes advocate a wet lab approach to a chemical problem!

At NCSSM, all instructors teach core chemistry courses – honors and AP – but also teach advanced electives, including organic, analytical, polymer, environmental, and industrial chemistry. In addition, we offer a program of instruction in chemical research. NCSSM is on a trimester schedule, meaning an elective course meets for 10-12 weeks from three to 5.5 hours per week.

Introduction to Computational Chemistry

In addition to the electives described above, I developed a trimester course “Introduction to Computational Chemistry”, a 30-hour program of instruction. A partial screenshot of the syllabus is shown below. The reader should note that I use the same general course description as that of a graduate level course at the University of Denver.

In this course, which routinely generates a waiting list of students wishing to participate, the focus is on both aspects of the “associative law” pedagogical approach. It is my goal in this course to provide students with the opportunity to learn how computation helps to solve challenging chemical problems. It is also my goal to provide students with the opportunity to learn the jargon, the foundational mathematics, and the methodology of computational chemistry. While some of our students will move to the university with the goal of being able to use computation as a tool for chemical learning and research – computational (chemistry research) -- all three of our local universities (Duke, University of North Carolina- Chapel Hill, and North Carolina State University) have extensive research programs in the development of new methods for doing computational chemistry. As such, and since many of our students matriculate to one of those three universities, it is my goal to prepare them to work in that developmental area of (computational chemistry) research.

In the Introduction to Computational Chemistry (Chem 412) course at NCSSM, I ask my students to be able to provide a meaningful discussion of the following questions by the end of the course (determined, of course, by the final exam!):

What is the role and purpose of computational chemistry? What does computational chemistry allow us to do that cannot be done using traditional (i.e. wet) chemistry?
What is the fundamental mathematical expression that needs to be solved in doing computational chemistry? What are the terms in this equation, what is their significance, what variations can be used?
What are the approximations that can be used in doing computational chemistry? What are the pros and cons of the various approximations? How does choice of approximation affect the results, computing time, etc.?
There are roughly four different "flavors" to computational chemistry: ab initio methods, semi-empirical methods, density functional theory (DFT) and molecular mechanics/molecular dynamics. What are these methods? How do they differ?
What are the fundamental units of measure used by computational chemists? What are some different ways that these fundamental units might be expressed?
What are some of the computer codes that one might use to do computational chemistry? What platforms are needed for these codes, what are the strengths and limitations of these codes?

Most if not all of these questions focus more on the (computational chemistry) education aspect, rather than the computational (chemistry education) part of the pedagogy. However, each student, generally working with a team of one or two other students, also completes a research project on a topic of interest to that group. Most of the students pick topics in which they are applying some technique of computational chemistry to an interesting chemical problem, while a few do studies that compare different computational approaches to some problem. Students must present their research in journal form, following the format of the Journal of Computational Chemistry (the same format used in the PDF version of this paper). A “Journal of Student Computational Chemistry” from the Spring 2007 semester can be found on the Web at http://chemistry.ncssm.edu/JcompChem.pdf.

The students in this class routinely (approximately once a week) read and discuss an article from the Journal of Computational Chemistry. Students are expected to learn how to read the primary scientific literature in this course, and be able to discuss their readings intelligently with me and with their fellow students.

The bottom part of the syllabus showing how this class is structured is provided below. NCSSM is unusual among high schools in that, since we are residential, we are able to provide evening classes. My course is held one night a week for three hours, so I need to structure it such that students are not subjected to a three-hour lecture! During the course of the class, they have a lecture, do an in-class lab, break out into small groups to discuss a journal article, and get instructions for the out-of-class lab that they must complete by the next week. We start with a 20-minute quiz on the previous week’s discussions and notes. Students are required to keep a lab notebook, and learn how a computational lab notebook is similar to but different from an experimental lab notebook. All NCSSM courses use the course management tool Moodle (http://moodle.org), an open-source (i.e., free) Web-based tool similar to Blackboard and WebCT.

Research in Computational Chemistry

Students who wish to continue their studies in computational chemistry can elect to take Chemistry 414, Research in Computational Chemistry. In this course, we explore more advanced techniques and tools, and students again conduct an independent research project, typically at a higher level than that of the project done in the Intro course. For this course, with its focus on the software program Gaussian 03 as the main computational engine, the course uses Exploring Chemistry with Electronic Structure Methods by James Foresman and Aeleen Frisch as the textbook.

This course has a support team of computational chemists at both Duke and UNC-Chapel Hill, consisting of post-doctoral students and research faculty. These researchers provide “just in time” support to me in answering questions that are out of my area of expertise, or work with students directly as needed. In addition to the use of standard computational chemistry tools (Gaussian, GAMESS, MOPAC), I also introduce other tools, such as AutoDock⁶, a protein docking software package developed by the Scripps Institute.

Sample projects for the current class include one student who working to improve the functionality of the WebMO interface by writing additional code; a student looking at the molecular structure of the compound responsible for the generation of oxygen through the Photosynthesis II process; and a student who has been working experimentally with the molecule heparin through a research program at UNC-Chapel Hill, and is doing an computational study of that molecule to augment his experimental work.

Medicinal Chemistry seminar

NCSSM also provides students and faculty with the opportunity to offer seminars based on personal interests, usually meeting once a week for 90 minutes. I offer a seminar in Medicinal Chemistry based on work I did earlier in my career in the area of anesthesiology and toxicology. In this seminar, which is completely computationally driven, students learn the basics of pharmacology, spend several weeks in drug design activities, and then spend several weeks looking at pharmacogenomics (using a variety of computational biology tools!). In one of the weekly computational labs, they do a small case study to determine the optimal geometry for the molecule acetylcholine, and conduct a potential energy scan (PES, also known as a coordinate scan) of that molecule:

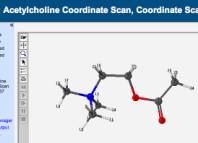
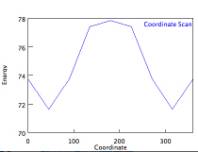
The seminar culminates with a large case study in which students must apply a variety of computational methods to the study of a medicinal compound. Playing one of several roles, students must work as a team to solve a complicated case study. A screenshot of the case study is shown below:

North Carolina’s Experiment

As mentioned earlier in this article, the computing tools used by my students were once only available on high performance computers, and thus off-limits to students, available only to research university and commercial scientists. As computers became more powerful and software was “ported” to desktop computers, the possibilities for students increased. At the undergraduate level, more chemistry departments began to establish computer labs with one or several computational chemistry software packages.

These tools, however, were simply too expensive or required computers not available to most high schools, even specialized schools such as NCSSM. In my own work, conversations with software vendors typically solicited the comment that high school students were simply not able to use their software. Even for those vendors (and they were few) who were supportive of pre-college efforts, they were unwilling or unable to provide the deep discounts that would be needed for high school budgets.

A number of efforts, such as the NSF-supported “ChemViz”⁷ program at the National Center for Supercomputing Applications (NCSA), developed access via the Web to computational chemistry tools and curricula for pre-college students. This resource, highly innovative in its time, did not provide students with powerful enough tools to do research. Nor did it have sufficient breadth and depth for teachers to be able to support a program of instruction in computational chemistry. At NCSSM, we were able to badger the software vendors enough to get software donated or at a very low cost. This model, however, was not sustainable for many high schools.

Over the years, a number of research-grade codes, such as MOPAC, GAMESS, and others became available for desktop computers and were in the public domain, meaning no cost. These software programs typically, however, required a significant understanding of computing systems (typically Unix/Linux) and also required students to learn a fairly cryptic system to generate input files for a calculation. For example, the code below is a sample input file for GAMESS:

$CONTRL SCFTYP=RHF RUNTYP=HESSIAN

ICHARG=0 MULT=1 COORD=ZMTMPC $END

$BASIS GBASIS=N21 NGAUSS=3 $END

$DATA

C15H12O6

C1 1

C 0.0000000 0 0.0000000 0 0.0000000 0 0 0 0

O 1.4341000 1 0.0000000 0 0.0000000 0 1 0 0

C 1.3718166 1 114.97905 1 0.0000000 0 2 1 0

C 1.4084832 1 123.81387 1 19.441139 1 3 2 1

C 1.3994155 1 118.83432 1 -179.85275 1 4 3 2

C 1.3841214 1 120.93122 1 -0.9970528 1 5 4 3

C 1.4067731 1 119.36659 1 -0.0927585 1 6 5 4

C 1.3980438 1 121.32708 1 0.8675006 1 7 6 5

H 1.0972631 1 120.91645 1 179.50426 1 8 7 6

O 1.3630382 1 115.97457 1 179.85347 1 7 8 3

H 0.9495488 1 108.20358 1 179.91360 1 10 7 8

H 1.0960879 1 120.74505 1 -179.38483 1 6 7 8

H 1.0973780 1 119.79391 1 179.52810 1 5 6 7

C 1.4733444 1 121.04055 1 176.87024 1 4 5 6

C 1.5473835 1 113.38224 1 -49.011031 1 1 2 3

O 1.4112240 1 110.11977 1 -64.884104 1 15 1 2

H 0.9480935 1 106.05570 1 -173.39745 1 16 15 1

H 1.1178096 1 108.10917 1 175.52041 1 15 1 2

O 1.2169777 1 120.33281 1 148.30413 1 14 15 1

C 1.5065672 1 107.29939 1 -174.25849 1 1 2 3

C 1.3945558 1 118.56470 1 -134.69061 1 20 1 2

C 1.3896935 1 120.57845 1 -179.66709 1 21 20 1

C 1.3987819 1 120.06596 1 -0.3073078 1 22 21 20

C 1.4148287 1 119.48882 1 0.1891373 1 23 22 21

C 1.3950668 1 121.41952 1 45.467224 1 20 1 2

H 1.0984649 1 119.57851 1 0.4094933 1 25 20 1

O 1.3686471 1 122.63812 1 179.88063 1 24 25 20

H 0.9494814 1 107.38800 1 0.5338152 1 27 24 25

O 1.3670389 1 117.63406 1 -179.85748 1 23 24 25

H 0.9495209 1 107.47905 1 -179.52436 1 29 23 24

H 1.0965534 1 120.42401 1 179.99587 1 22 23 24

H 1.0961999 1 120.19317 1 0.4409991 1 21 20 1

H 1.1201156 1 106.49306 1 68.559180 1 1 2 3

$END

Needless to say, having students create these types of input files was, and is, an unrealistic expectation, even for the most advanced students (although we did that for several years, not much fun for all concerned).

So the problems of getting computational chemistry tools into the hands of students were substantial. Software that was too expensive, requiring advanced computer knowledge to install, and input files that were very difficult to create added up to an untenable situation for most teachers. These problems, however, were solved (at least for us in North Carolina) with the advent of the WebMO interface.

WebMO is a Java-based tool that provides users with a very easy to use interface to a number of computational packages, including Gaussian 03, MOPAC, GAMESS, and others, such as Tinker and NWChem. The interface can be taught in one class session, and provides advanced users with the option to customize jobs by hand. Most users, however, use the pull-down menus that come with the software and that can be customized by the system administrator.

With funding from the Burroughs Wellcome Fund (http://bwfund.org) and the North Carolina Science, Mathematics and Technology Center (http://www.ncsmt.org/), we purchased a Dell dual-processor Linux server, a commercial version of WebMO, and a license for Gaussian 03, with a total cost of about $5,000. In addition to Gaussian 03, we installed the GAMESS, MOPAC, and Tinker public domain codes on the server. This resource is now available to any pre-college teacher and student physically resident in the State of North Carolina. Teachers can request classroom accounts, where each student receives an amount of computing time, limited to small jobs (under four minutes) with a total time limit (30 minutes). Students can request research accounts by submitting a research proposal to me, following the format used to request computing time on supercomputers and other high-performance (“big iron”) computing systems.

In the two years since its establishment, the server has accommodated hundreds of students for more than 16,000 jobs. In addition to courses offered at NCSSM (and described earlier), classes in computational chemistry are offered via NCSSM’s extensive distance learning program (http://www.dlt.ncssm.edu/distance_learning/DLWorkshops/ComputationaChemistry_Fall-07.pdf).

The main advantage of this system is that all of the installation and maintenance of the system is done by NCSSM scientists and system administrators, and is provided to all schools at no cost. In addition, schools do not have to install any software, often a problem in North Carolina’s public schools. Schools only need access to Java-enabled Web browsers, a technology available to the majority of North Carolina’s schools.

In working to get more teachers aware of and able to use the resources, I offered (and continue to offer) workshops at various conferences such as the North Carolina Science Teachers Association annual conference. In talking with teachers, it was clear that there was limited travel time and funding to attend workshops to learn how to do computational chemistry. To attempt to address that issue, and with additional generous funding from BWF and the NCSMT Center, a colleague (Dr. Shawn Sendlinger at North Carolina Central University) and I collaborated to write an electronic textbook entitled A Chemistry Educator’s Guide to Molecular Modeling (http://chemistry.ncssm.edu/book). This book (with some chapters still in writing) looks to provide teachers with enough background in both areas of computational chemistry (methodology and pedagogy) to integrate computation into their own classrooms. I use this book in my “Introduction to Computational Chemistry” course, in spite of the fact that it is written primarily for chemistry educators.

National Resources: The Global Grid Exchange

In addition to doing workshops and distance learning programs across the state of North Carolina, I have been giving talks and workshops outside of North Carolina. During these workshops, the main focus has been on how participants might set up a WebMO-based server for their own schools, region, and/or state. After several of these workshops, I was able to arrange for seed funding from BWF to help others who might wish to replicate the North Carolina resources.

About the same time, Parabon Computation, Inc. (http://www.parabon.com/), a grid computing organization based in Reston, VA, contacted me about providing grid resources for educational purposes. In grid computing, computing jobs are distributed to idle computers, to be run when those personal computers are not in use by the owner. The results of the job are then sent back to the host computer for analysis by the originator.

With support funding from Cisco Systems, we established a mirror site (http://cli.globalgridexchange.com/) of the North Carolina machine. On the grid computer, we have installed the WebMO interface and access to GAMESS, MOPAC, and Tinker, along with a link to the electronic textbook, labs, and other resources. Due to licensing constraints, Gaussian 03 is not available on this machine.

This new and greatly appreciated resource now allows NCSSM to provide free classroom and student research accounts to any pre-college teacher or student in the United States. Professional staff at NCSSM and Parabon maintain both the North Carolina and national servers, with additional support from a team of six computational chemistry high school interns at NCSSM.

Even with these resources in place, it is clear that many teachers will want and need additional support prior to implementing computational chemistry in their classrooms. We are hoping to be able to provide significant support, in the form of FAQs (frequently asked questions) pages, an increasing number of ready-to-go labs, and the sharing of the curricular materials developed over the past many years. With these resources, I am hopeful that teachers will feel empowered to add a few activities a year to their classes, and perhaps consider offering a course in computation at their schools. I am also hopeful that newly trained teachers will develop their own computational chemistry classroom and lab activities to be shared with the larger community.

Conclusions

The main premise of this paper is that it is critically important that tomorrow’s chemical scientists understand the technologies, techniques and tools of computational chemistry. With the resources now available – access to research-grade hardware and software at no cost, an ever-increasing body of labs and curricular materials, and other support mechanisms – it is the hope of this author that computational chemistry will as familiar to tomorrow’s chemistry researchers and teachers as the test tube and the beaker are now.

Acknowledgements

Appreciation is extended to the Burroughs Wellcome Fund and the North Carolina Science, Mathematics and Technology Center for their funding support for the North Carolina High School Computational Server. Appreciation is also expressed to the Global Grid Exchange, Parabon Computation, Inc. (http://www.parabon.com/) and Cisco Systems (http://www.cisco.com/) for their support of the national computational chemistry server.

References

1. MOPAC Version 7.00, J. J. P. Stewart, Fujitsu Limited, Tokyo, Japan.

2. The North Carolina High School Computational Chemistry Server, http://chemistry.ncssm.edu.

3. Schmidt, J.R.; Polik, W.F. WebMO Pro, version 7.0; WebMO LLC: Holland, MI, USA, 2007; available from http://www.webmo.net (accessed April 2007).

4. Gaussian 03, Revision C.02, M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, J. A. Montgomery, Jr., T. Vreven, K. N. Kudin, J. C. Burant, J. M. Millam, S. S. Iyengar, J. Tomasi, V. Barone, B. Mennucci, M. Cossi, G. Scalmani, N. Rega, G. A. Petersson, H. Nakatsuji, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, M. Klene, X. Li, J. E. Knox, H. P. Hratchian, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, P. Y. Ayala, K. Morokuma, G. A. Voth, P. Salvador, J. J. Dannenberg, V. G. Zakrzewski, S. Dapprich, A. D. Daniels, M. C. Strain, O. Farkas, D. K. Malick, A. D. Rabuck, K. Raghavachari, J. B. Foresman, J. V. Ortiz, Q. Cui, A. G. Baboul, S. Clifford, J. Cioslowski, B. B. Stefanov, G. Liu, A. Liashenko, P. Piskorz, I. Komaromi, R. L. Martin, D. J. Fox, T. Keith, M. A. Al-Laham, C. Y. Peng, A. Nanayakkara, M. Challacombe, P. M. W. Gill, B. Johnson, W. Chen, M. W. Wong, C. Gonzalez, and J. A. Pople, Gaussian, Inc., Wallingford CT, 2004.

5. "General atomic and molecular electronic structure system, M.W.Schmidt, K.K.Baldridge, J.A.Boatz, S.T.Elbert, M.S.Gordon, J.H.Jensen, S.Koseki, N.Matsunaga, K.A.Nguyen, S.J.Su, T.L.Windus, M.Dupuis, J.A.Montgomery, Journal of Computational Chemistry, vol. 14, pages 1347-1363, 1993."

6. Morris, G.M., Goodsell, D.S., Halliday, R.S., Huey, R, Hart, W.E., Belew, R.K., Olson, A.J. (1998) Automated docking using Lamarckian genetic algorithm and an empirical binding free energy function. J. Comp. Chem. 19:1639-1662.

7. ChemViz, National Center for Supercomputing Applications (NCSA), University of Illinois at Urbana-Champaign, http://chemviz.ncsa.uiuc.edu/

North Carolina School of Science and Mathematics, Durham, NC